Треугольник — хорошо знакомая всем фигура. И это, несмотря на богатое разнообразие его форм. Прямоугольный, равносторонний, остроугольный, равнобедренный, тупоугольный. Каждый из них чем-то отличается. Но для любого требуется узнавать площадь треугольника.

Общие для всех треугольников формулы, в которых используются длины сторон или высот

Обозначения, принятые в них: стороны — а, в, с; высоты на соответствующие стороны н а, н в, н с.

1. Площадь треугольника вычисляется, как произведение ½, стороны и высоты, опущенной на нее. S = ½ * а * н а. Аналогично следует записать формулы для двух остальных сторон.

2. Формула Герона, в которой фигурирует полупериметр (его принято обозначать маленькой буквой р, в отличии от полного периметра). Полупериметр необходимо сосчитать так: сложить все стороны и разделить их на 2. Формула полупериметра: р = (а+в+с) / 2. Тогда равенство для площади фигуры выглядит так: S = √ (р * (р - а) * (р - в) * (р - с)).

3. Если не хочется использовать полупериметр, то пригодится такая формула, в которой присутствуют только длины сторон: S = ¼ * √ ((а + в + с) * (в + с - а) * (а + с - в) * (а + в - с)). Она несколько длиннее предыдущей, но выручит, если забылось, как находить полупериметр.

Общие формулы, в которых фигурируют углы треугольника

Обозначения, которые требуются для прочтения формул: α, β, γ — углы. Они лежат напротив сторон а, в, с, соответственно.

1. По ней половина произведения двух сторон и синуса угла между ними равна площади треугольника. То есть: S = ½ а * в * sin γ. Подобным образом следует записать формулы для двух других случаев.

2. Площадь треугольника можно вычислить по одной стороне и трем известным углам. S = (а 2 * sin β * sin γ) / (2 sin α).

3. Существует еще формула с одной известной стороной и двумя прилежащими к ней углами. Она выглядит таким образом: S = с 2 / (2 (ctg α + ctg β)).

Две последние формулы являются не самыми простыми. Запомнить их довольно сложно.

Общие формулы для ситуации, когда известны радиусы вписанных или описанных окружностей

Дополнительные обозначения: r, R — радиусы. Первый используется для радиуса вписанной окружности. Второй — для описанной.

1. Первая формула, по которой вычисляется площадь треугольника, связана с полупериметром. S = р * r. По-другому ее можно записать так: S = ½ r * (а + в + с).

2. Во втором случае потребуется перемножить все стороны треугольника и разделить их на учетверенный радиус описанной окружности. В буквенном выражении это выглядит так: S = (а * в * с) / (4R).

3. Третья ситуация позволяет обойтись без знания сторон, но потребуются значения всех трех углов. S = 2 R 2 * sin α * sin β * sin γ.

Частный случай: прямоугольный треугольник

Это самая простая ситуация, поскольку требуется знание только длины обоих катетов. Они обозначаются латинскими буквами а и в. Площадь прямоугольного треугольника равна половине площади достроенного к нему прямоугольника.

Математически это выглядит так: S = ½ а * в. Она запоминается проще всего. Потому что выглядит, как формула для площади прямоугольника, только появляется еще дробь, обозначающая половину.

Частный случай: равнобедренный треугольник

Поскольку у него две стороны равные, то некоторые формулы для его площади выглядят несколько упрощенными. Например, формула Герона, по которой вычисляется площадь равнобедренного треугольника, принимает следующий вид:

S = ½ в √((a + ½ в)*(a - ½ в)).

Если ее преобразовать, то она станет короче. В таком случае формула Герона для равнобедренного треугольника записывается так:

S = ¼ в √(4 * a 2 - b 2).

Несколько проще, чем для произвольного треугольника, выглядит формула площади, если известны боковые стороны и угол между ними. S = ½ a 2 * sin β.

Частный случай: равносторонний треугольник

Обычно в задачах про него известна сторона или ее можно как-либо узнать. Тогда формула, по которой находится площадь такого треугольника, выглядит следующим образом:

S = (а 2 √3) / 4.

Задачи на нахождение площади, если треугольник изображен на клетчатой бумаге

Самой простой является ситуация, когда прямоугольный треугольник начерчен так, что его катеты совпадают с линиями бумаги. Тогда требуется просто посчитать число клеточек, укладывающихся в катеты. Потом перемножить их и разделить на два.

Когда треугольник остроугольный или тупоугольный, его нужно дорисовать до прямоугольника. Тогда в получившейся фигуре будет 3 треугольника. Один — тот что дан в задаче. А два других — вспомогательные и прямоугольные. Определить площади двух последних нужно по описанному выше способу. Потом сосчитать площадь прямоугольника и вычесть из него те, что вычислены для вспомогательных. Площадь треугольника определена.

Гораздо сложнее оказывается ситуация, в которой ни одна из сторон треугольника не совпадает с линиями бумаги. Тогда его нужно вписать в прямоугольник так, чтобы вершины исходной фигуры лежали на его сторонах. В этом случае вспомогательных прямоугольных треугольников будет три.

Пример задачи на формулу Герона

Условие. У некоторого треугольника известны стороны. Они равны 3, 5 и 6 см. Необходимо узнать его площадь.

Теперь можно вычислять площадь треугольника по указанной выше формуле. Под квадратным корнем оказывается произведение четырех чисел: 7, 4, 2 и 1. То есть площадь равна √(4 * 14) = 2 √(14).

Если не требуется большая точность, то можно извлечь квадратный корень из 14. Он равен 3,74. Тогда площадь будет равна 7,48.

Ответ. S = 2 √14 см 2 или 7,48 см 2 .

Пример задачи с прямоугольным треугольником

Условие. Один катет прямоугольного треугольника больше, чем второй на 31 см. Требуется узнать их длины, если площадь треугольника равна 180 см 2 .
Решение. Придется решить систему из двух уравнений. Первое связано с площадью. Второе — с отношением катетов, которое дано в задаче.
180 = ½ а * в;

а = в + 31.
Сначала значение «а» нужно подставить в первое уравнение. Получится: 180 = ½ (в + 31) * в. В нем только одна неизвестная величина, поэтому его легко решить. После раскрытия скобок получается квадратное уравнение: в 2 + 31 в - 360 = 0. Оно дает два значения для «в»: 9 и - 40. второе число не подходит в качестве ответа, так как длина стороны треугольника не может быть отрицательной величиной.

Осталось вычислить второй катет: прибавить к полученному числу 31. Получается 40. Это искомые в задаче величины.

Ответ. Катеты треугольника равны 9 и 40 см.

Задача на нахождение стороны через площадь, сторону и угол треугольника

Условие. Площадь некоторого треугольника 60 см 2 . Необходимо вычислить одну из его сторон, если вторая сторона равна 15 см, а угол между ними равен 30º.

Решение. Исходя из принятых обозначений, искомая сторона «а», известная «в», заданный угол “γ”. Тогда формула площади можно переписать так:

60 = ½ а * 15 * sin 30º. Здесь синус 30 градусов равен 0,5.

После преобразований «а» оказывается равным 60 / (0,5 * 0,5 * 15). То есть 16.

Ответ. Искомая сторона равна 16 см.

Задача о квадрате, вписанном в прямоугольный треугольник

Условие. Вершина квадрата со стороной 24 см совпадает с прямым углом треугольника. Две другие лежат на катетах. Третья принадлежит гипотенузе. Длина одного из катетов равна 42 см. Чему равна площадь прямоугольного треугольника?

Решение. Рассмотрим два прямоугольных треугольника. Первый — заданный в задаче. Второй — опирается на известный катет исходного треугольника. Они подобны, так как имеют общий угол и образованы параллельными прямыми.

Тогда отношения их катетов равны. Катеты меньшего треугольника равны 24 см (сторона квадрата) и 18 см (заданный катет 42 см вычесть сторону квадрата 24 см). Соответствующие катеты большого треугольника — 42 см и х см. Именно этот «х» нужен для того, чтобы вычислить площадь треугольника.

18/42 = 24/х, то есть х = 24 * 42 / 18 = 56 (см).

Тогда площадь равна произведению 56 и 42, разделенному на два, то есть 1176 см 2 .

Ответ. Искомая площадь равна 1176 см 2 .

Порой в жизни встречаются такие ситуации, когда приходится копаться в памяти в поисках давно забытых школьных знаний. Например, нужно определить площадь земельного участка треугольной формы или же пришел черед очередного ремонта в квартире или частном доме, и нужно посчитать, сколько уйдет материала для поверхности с треугольной формой. Было время, когда вы могли решить такую задачку за пару минут, а теперь отчаянно пытаетесь вспомнить, как же определить площадь треугольника?

Не стоит из-за этого переживать! Ведь это вполне нормально, когда мозг человека решает переложить давно неиспользуемые знания куда-нибудь в удаленный уголок, из которого порой их не так-то и легко извлечь. Чтобы вам не пришлось мучиться с поиском забытых школьных знаний для решения такой задачи, в этой статье собраны различные методы, которые позволяют легко найти искомую площадь треугольника.

Общеизвестно, что треугольником называют такой вид многоугольника, который ограничен минимально возможным количеством сторон. В принципе, любой многоугольник можно разделить на несколько треугольников, соединив его вершины отрезками, которые не пересекают его стороны. Поэтому, зная треугольника, можно посчитать площадь практически любой фигуры.

Среди всех возможных треугольников, которые встречаются в жизни, можно выделить следующие частные виды: и прямоугольный.

Проще всего площадь треугольника рассчитывается, когда один из его углов прямой, то есть в случае с прямоугольным треугольником. Несложно заметить, что он представляет собой половину прямоугольника. Поэтому его площадь равна половине произведения сторон, которые образуют между собой прямой угол.

Если нам известны высота треугольника, опущенная из одной из его вершин на противоположную сторону, и длина этой стороны, которую называют основанием, то площадь рассчитывается как половина произведения высоты на основание. Записывается это с помощью такой формулы:

S = 1/2*b*h, в которой

S - искомая площадь треугольника;

b, h - соответственно, высота и основание треугольника.

Так легко рассчитать площадь равнобедренного треугольника, поскольку высота будет делить противоположную сторону пополам, и ее легко можно будет измерить. Если определяется площадь то в качестве высоты удобно брать длину одной из сторон, образующих прямой угол.

Все это конечно хорошо, но как определить, является ли один из углов треугольника прямым или нет? Если размер нашей фигуры небольшой, то можно воспользоваться строительным углом, чертежным треугольником, открыткой или другим предметом с прямоугольной формой.

Но что делать, если у нас треугольный земельный участок? В этом случае поступают следующим образом: отсчитывают от вершины предполагаемого прямого угла по одной из сторон расстояние кратное 3 (30 см, 90 см, 3 м), а по другой стороне отмеряют в той же пропорции расстояние кратное 4 (40 см, 160 см, 4 м). Теперь нужно измерить расстояние между конечными точками этих двух отрезков. Если получилось значение кратное 5 (50 см, 250 см, 5 м), то можно утверждать, что угол прямой.

Если известно значение длины каждой из трех сторон нашей фигуры, то площадь треугольника можно определить, используя формулу Герона. Для того чтобы она имела более простой вид, применяют новую величину, которая называется полупериметром. Это сумма всех сторон нашего треугольника, разделенная пополам. После того как полупериметр посчитан, можно приступать к определению площади по формуле:

S = sqrt(p(p-a)(p-b)(p-c)), где

sqrt - квадратный корень;

p - значение полупериметра (p =(a+b+c)/2);

а,b,с - ребра (стороны) треугольника.

Но что делать, если треугольник имеет неправильную форму? Здесь возможны два способа. Первый из них состоит в том, чтобы попытаться разделить такую фигуру на два прямоугольных треугольника, сумму площадей которых посчитать отдельно, а затем сложить. Или же, если известен угол между двумя сторонами и размер этих сторон, то применить формулу:

S = 0.5 * ab * sinC, где

a,b - стороны треугольника;

с - величина угла между этими сторонами.

Последний случай на практике встречается редко, но тем не менее, в жизни все возможно, поэтому приведенная выше формула не будет лишней. Удачи в расчётах!

Площадь треугольника. Во многих задачах по геометрии связанных с вычислением площадей используются формулы площади треугольника. Их существует несколько, здесь мы рассмотрим основные. Перечислить эти формулы было бы слишком просто и пользы ни какой. Мы разберём происхождение основных формул, тех что используются наиболее чаще.

Перед тем как ознакомиться с выводом формул обязательно посмотрите статью о . После изучения материала вы без труда сможете восстановить формулы в памяти (если вдруг они «вылетят» в нужный вам момент).

Первая формула

Диагональ параллелограмма разбивает его на два равных по площади треугольника:

Следовательно площадь треугольника будет равна половине площади параллелограмма:

Площадь треугольника формула

*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.

Формула вторая

Как уже было изложено в статье о площади параллелограмма формула имеет вид:

Площадь треугольника равна половине его площади, значит :

*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.

Формула Герона (третья)

Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.

*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.

Формула четвёртая

где r – радиус вписанной окружности

*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.

Формула пятая

где R – радиус описанной окружности.

*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.

Возникает вопрос: если известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!

Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются в составе ЕГЭ.

Давайте отдельно рассмотрим формулу:

Она является частным случаем формулы площади многоугольника, в который вписана окружность:

Рассмотрим её на примере пятиугольника:

Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём опущенные перпендикуляры являются радиусами вписанной окружности:

Площадь пятиугольника равна:

Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:

Формула шестая

Площадь треугольника - формулы и примеры решения задач

Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.

Примечание . Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:

• "Формулы площади равностороннего треугольника"

Формулы площади треугольника

Пояснения к формулам :
a, b, c - длины сторон треугольника, площадь которого мы хотим найти
r - радиус вписанной в треугольник окружности
R - радиус описанной вокруг треугольника окружности
h - высота треугольника, опущенная на сторону
p - полупериметр треугольника, 1/2 суммы его сторон (периметра)
α - угол, противолежащий стороне a треугольника
β - угол, противолежащий стороне b треугольника
γ - угол, противолежащий стороне c треугольника
h a , h b , h c - высота треугольника, опущенная на сторону a , b , c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

• Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
• Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
• Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
• Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
• Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
• Формула Герона (6) - это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
• Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
• Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула 8)
• Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
• Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
• Формула 11 позволяет вычислить площадь треугольника по координатам его вершин , которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

Примечание . Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет - пишите об этом в форуме. В решениях вместо символа "квадратный корень" может применяться функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение . Иногда для простых подкоренных выражений может использоваться символ √

Задача. Найти площадь по двум сторонам и углу между ними

Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника .

Решение .

Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ

Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60

В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов . Он будет равен корню из трех на два.
S = 15 √3 / 2

Ответ : 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)

Задача. Найти площадь равностороннего треугольника

Найти площадь равностороннего треугольника со стороной 3см.

Решение .

Площадь треугольника можно найти по формуле Герона:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Поскольку a = b = c формула площади равностороннего треугольника примет вид:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

Ответ : 9 √3 / 4.

Задача. Изменение площади при изменении длины сторон

Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?

Решение .

Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.

Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.

Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(см. первую строку рисунка внизу)

Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:

S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(см. вторую строку на рисунке внизу)

Как видно, 4 - общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - на третьей строке рисунка
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - четвертая строка

Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(см. пятую строку рисунка внизу)

Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.

Понятие площади

Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.

Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.

Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.

Рассмотрим пример.

Пример 1

Очевидно, что одна из сторон треугольника является диагональю прямоугольника , у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

Тогда площадь треугольника равняется

Ответ: $15$.

Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ - длина стороны, $h$ - высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

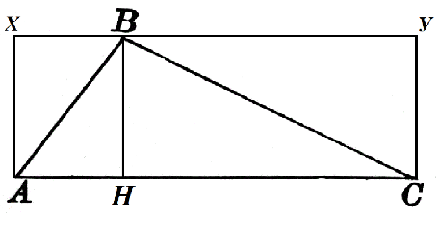
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Формула Герона

Теорема 2

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника.

Доказательство.

Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

Из треугольника $CBH$, по теореме Пифагора, имеем

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Из этих двух соотношений получаем равенство

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac{γ^2-α^2+β^2}{2β}$

$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$

$h^2=\frac{(α^2-(γ-β)^2)((γ+β)^2-α^2)}{4β^2}$

$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$

Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит

$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$

$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$

$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$

$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

По теореме 1, получим

$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$